For the last few months I’ve been trying out a solver for the popular web game Wordle, hosted by the New York Times. The game is a guessing game for a five-letter dictionary word, where your guesses also have to be valid words and feedback comes from colored feedback from each letter:

Letters that aren’t in the final word are black, letters that are in the word but are in the wrong place are yellow, and totally correct letters are green.
As well as playing myself normally, I’ve also coded a solution that seems to work in a very regular pattern:
How does my code work? First, we need a list of words. Since I’m writing this in python, I’m using a python NLP library and only taking the five-letter words from its dictionary.
With a word list in hand, it’s only a matter of carving up the list by giving the game valid guesses until only one guess remains!
When performing a binary search, we consult the halfway point of an ordered list and see if our desired value is above or below that, and discard the half that definitely doesn’t fit. With multiple variables in play, five letters that could have each one of twenty six values, we can optimally do much better than simply halving the list each time.
For my solution, I consulted information theory. We want the most bits of information with each play to make the guess that, in the average case, narrow down the word list the most. That meant simulating each word as a guess against each word as an answer, and comparing average remaining guess lengths. By seeing how much the expected list will shrink from the current word list, we can calculate how many bits each answer will give us, and take the one that will probably give us the most.
As you might expect from reading the description of the algorithm, the first hurdle comes from exponents. If we’re comparing 5 items, we have to make 25 comparisons, but if we’re comparing 30 items we’ll have to make 900 comparisons. It’s an O^2 solution.
For the first guess, we’ll always have the same amount of information (none), so I’ve calculated that “RAISE” gives the most bits of information in most cases. As a Scrabble player, this makes sense. Tiles there that have lower points are very common. Other players use it, along with similar words like “AUDIO” and “ADIEU”. Anyway, having calculated the best first guess for my parameters, I’ve hard-coded it to save time.
To prevent long calculations in the game itself, I took the task of finding best guesses for very long lists of words and broke it up by making many smaller lists and finding the best guess for these, and using the modal best answer from those. This is much faster, but while the answer for these smaller sets isn’t always the best for the whole set, it’s usually in the top ten.
The second computational hurdle is situations where we know all but a few letters, so the best guess from among them may take longer than we have guesses. Say we know that the word resembles “-OULD”, which means it could be “BOULD”, “COULD”, “GOULD”, “HOULD”, “MOULD”, “NOULD”, “TOULD” or “WOULD”. Any guess from these words would eliminate only itself! In these cases we should look again at the whole word list and find a word that’ll eliminate more guesses for us, even if it itself can’t be a solution. Here, the best play might be “CHANT”, which can give a result on four of the above words at the same time.

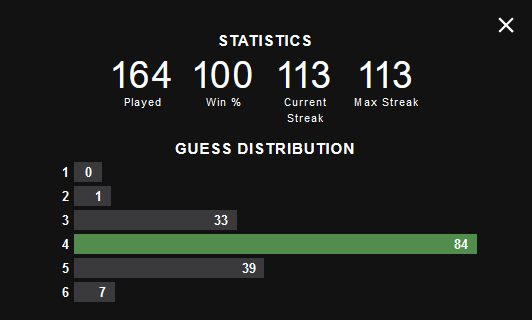
I consider the above puzzle to be the perfect test that my code is ready for publishing — This above word was only figured out by 40% of total players, as opposed to over 97% of usual words. And it did so in only four turns, as it does with most cases! And much faster than the NYT’s own bot built by statisticians!
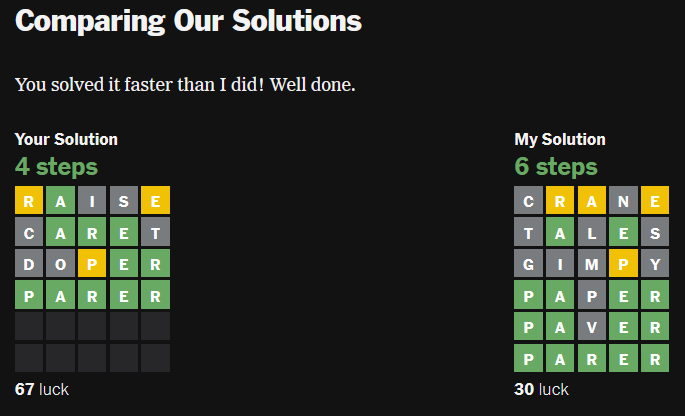
That same bot said my bot used little skill and mostly luck, I say I’ve got the receipts to show otherwise!
I built this, so it’s not cheating when I use it,
John